Fractals
As a personal challenge I set out to implement the menger sponge in Houdini. To make things a little trickier I decided to try for a volume implementation and a geometry implementation.
As a Volume
From a node perspective the volume implementation is pretty simple. A single volume wrangle controls the fractal and a vdb convert node converts it into an SDF. I would have liked to implement this as a recursive function, but I found that vex actually doens’t support that. In any case this looping method is probably safer.
int menger(vector origin; vector pos; int total_iterations; vector size){
for(int iteration = 1; iteration <= total_iterations; iteration++){
// Calculate the width of the current box
vector cur_width;
cur_width = size/pow(3, (iteration-1));
// Query which section of the current box the voxel lives in
// 0, 1, or 2 on each axis
vector remapped = fit(pos, origin, origin+cur_width, {0,0,0}, {1,1,1});
vector box = abs(floor((remapped)*{3,3,3}));
// This iteration says this voxel is solid
if((abs(box.x-1) + abs(box.y-1) + abs(box.z-1)) > 1){
// Redefine origin for next loop
origin = origin+(cur_width/3)*box;
}
else{
return 0;
}
}
return 1;
}
vector origin = chv("origin");
@density = menger(origin, @P, chi("iterations"), chv("size"));
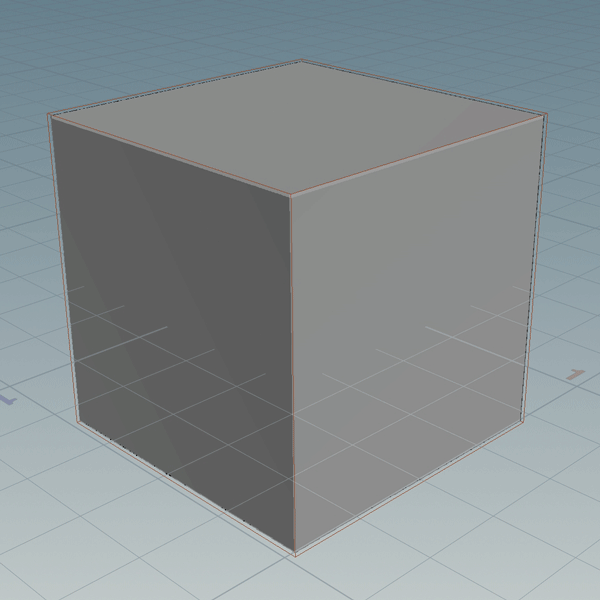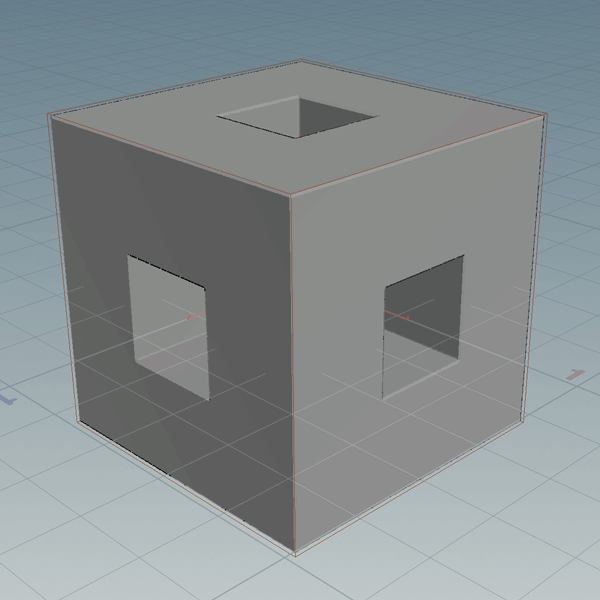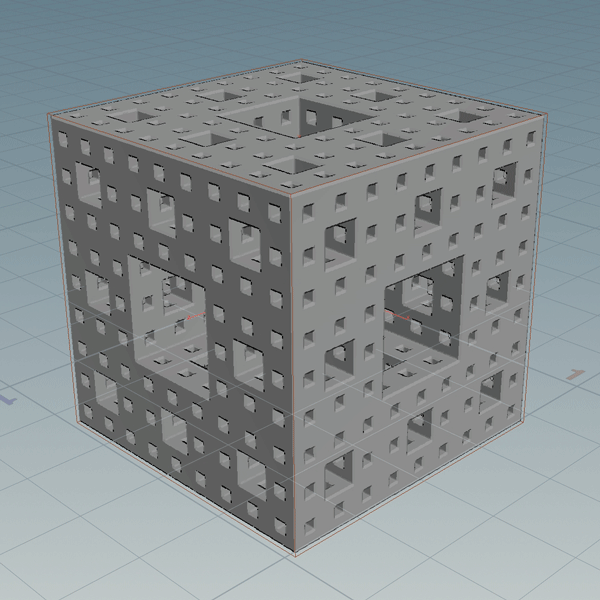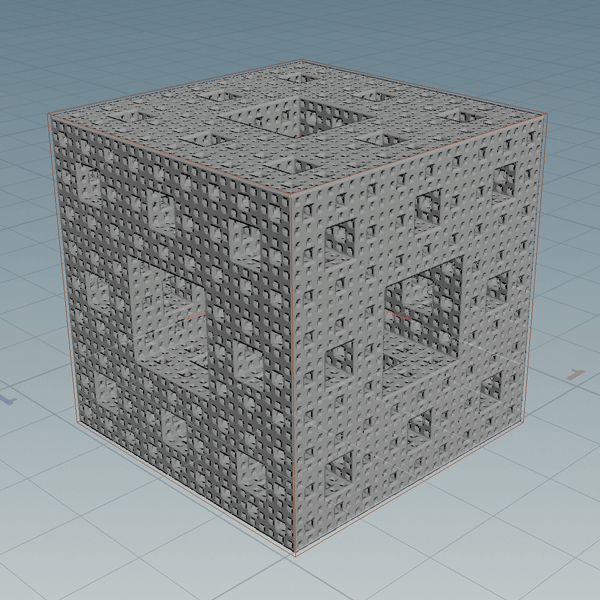
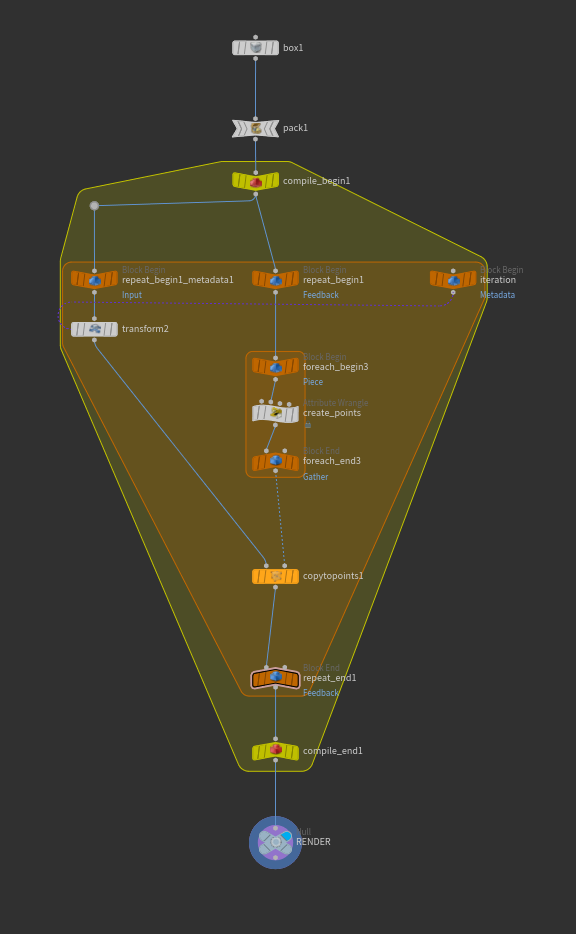
As Geo
Not surprisingly the geometry implementation is significantly faster. It only makes one query for each box instead of for each unit of space within each box. The basic structure is two nested for loops. The outer for each iteration and the inner for each box in that iteration. This was a great usecase for Houdini’s parallel processing compiled blocks. Even the 4th iteration generates in just a couple seconds. The fifth generation takes longer to display in the viewport than it does to generate.
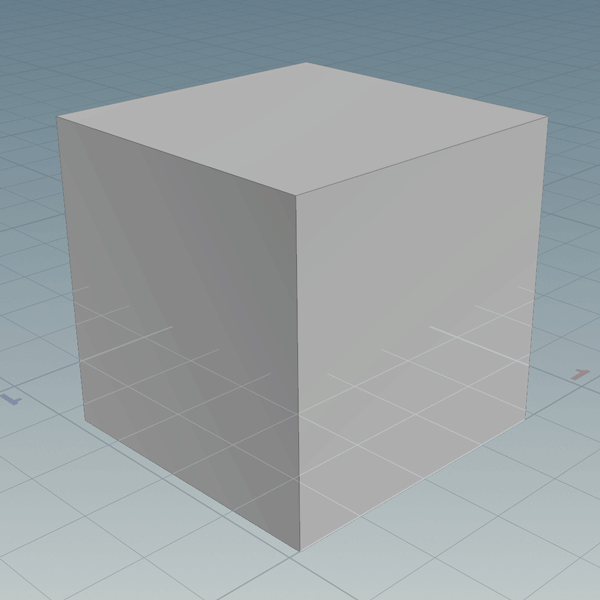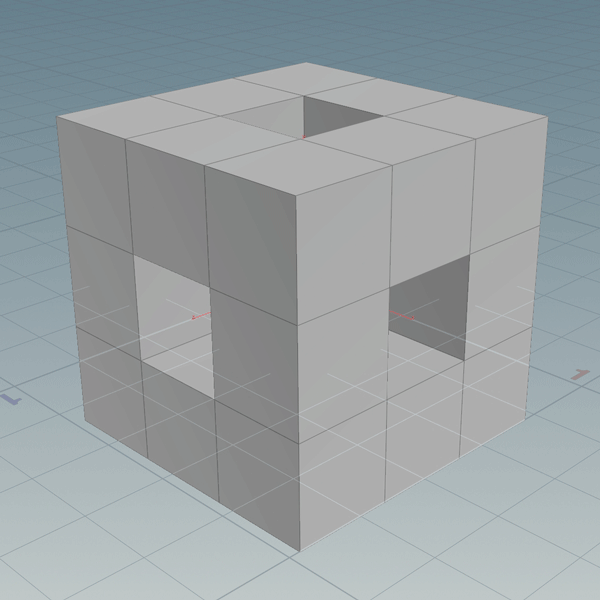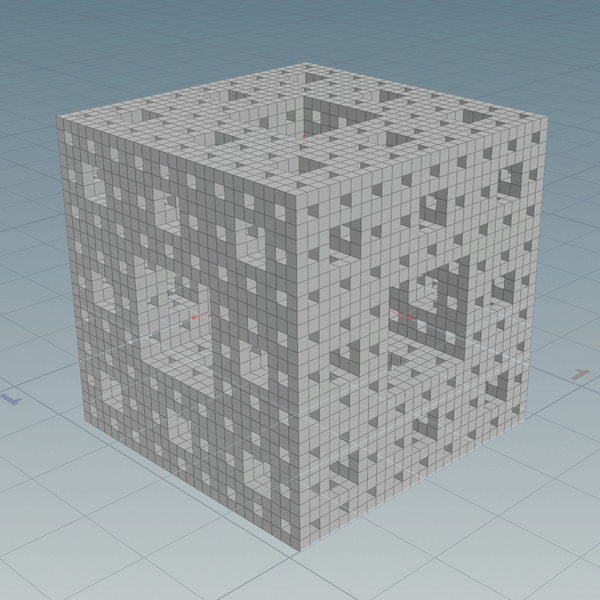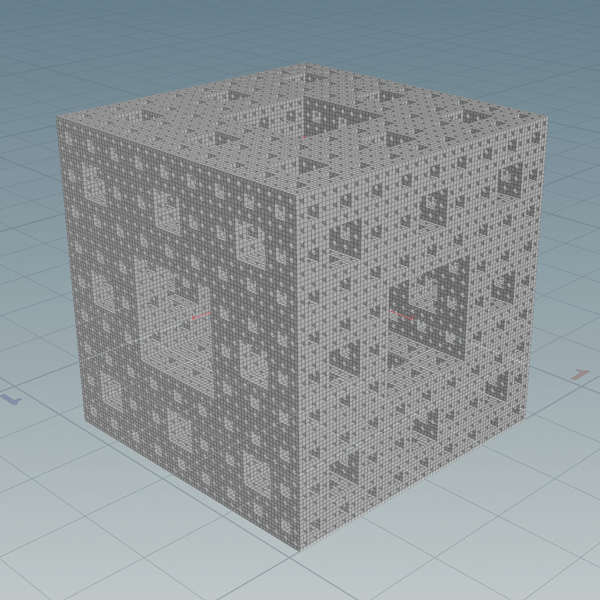
Download hip file
Links
Coding challenge for building a menger sponge